A determinação das quatro soluções da equação quártica simétrica
é bastante fácil, como passo a explicar. Não sendo o termo constante nulo
não é raíz da equação. Dividindo por
fica
Fazendo a seguinte mudança de variáveis
obtemos
e
Esta equação em tem as duas raízes
Resolvendo em ordem a
, tem-se
donde as quatro soluções de são
e
Artigo relacionado: Resolução da equação do 4.º grau (ou quártica)










Acho que há um erro nessa solução, depois de dividir por x^2 e colocar em evidência o indice a foi repetido pois esta em evidencia com o x^2 e x^-2 aparecendo novamente no final sozinho junto ao indice c.
Obrigado. Corigi nas duas equações onde estava a mais. A 2.ª equação em estava correcta, pelo que esta gralha não se repercutiu nas soluções
estava correcta, pelo que esta gralha não se repercutiu nas soluções 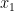 a
a 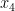 .
.