Formulário

NOTAÇÃO

Fim de demonstração

$\blacksquare$ ou $\square$

Fim da resolução de um problema ou exemplo

$\blacktriangleleft$

Início da explicação de um exemplo

$\blacktriangleright$

Factorial de $n$

$n!=1\times 2\times 3\times \cdots \times \left( n-1\right) \times n$

Coeficiente binomial $\displaystyle\dbinom{n}{k}=^{n\!}C_{k}=\dfrac{n!}{k!\left( n-k\right) !}=\dfrac{n\left( n-1\right)\left( n-2\right) \cdots \left( n-k+1\right) }{k!}$

Parte inteira (maior inteiro menor ou igual a) de $x$

$\displaystyle\lfloor x \rfloor$

Divide ( $p$ divide $q$ ou $q$ é múltiplo de $p$ )

$\mid$ Exemplo: $p\mid q$

Somatório (uma soma com um número finito de parcelas)

$\displaystyle\sum_{i=m}^{n}a_{i}=\sum_{m\leq i\leq n}a_{i}= a_{m}+a_{m+1}+a_{m+2}+\cdots +a_{n}$

Função trigonométrica seno de $x$

$\text{sen}\; x$ ou $\sin x$

Função trigonométrica tangente de $x$

$\text{tg}\; x$ ou $\tan x$

Função trigonométrica inversa arco seno de $x$

$\text{arcsen}\; x$ ou $\arcsin x$

Função trigonométrica inversa arco tangente de $x$

$\text{arctg}\; x$ ou $\arctan x$

Inclusão (elemento de, pertence); exemplo: $x$ é real

$x\in\mathbb{R}$

Diferença entre; exemplos:

$F\left( x\right) |_{a}^{b}=F\left( b\right) -F\left( a\right)$ ou $\left[ F(x)\right] _{a}^{b}=F\left( b\right) -F\left( a\right)$

$a_{i}|_{m}^{n}=a_{n}-a_{m}$

Limites; exemplos:

$\displaystyle\lim_{x \to a}f (x)$

$\displaystyle\lim_{n \to +\infty}u_n$

Integral (ou Primitiva)

$\displaystyle\int$ ou $P$

Norma da função real $f(x)$

$||f||=(f,f)^\frac{1}{2}=(f\cdot f)^\frac{1}{2}=\displaystyle\sqrt{\displaystyle\int_I [f(x)]^2\;dx}$ .

Produto interno de duas funções complexas $f,g$

$(f,\overline{g})=(f\cdot\overline{g})=\displaystyle\int_I f(x)\overline{g(x)}\;dx$

Norma da função complexa $f$

$||f||=(f,\overline{f})=(f\cdot\overline{f})=\displaystyle\int_I f(x)\overline{f(x)}\;dx$

Transformada de Laplace da função $F(t)$

$\mathcal{L}\left\{ F\left( t\right) \right\} =\displaystyle\int_{0}^{\infty }e^{-st}F\left( t\right)\;dt$

Valoração $p$ -ádica de $n$

$v_{p}(n)$

Fracções contínuas

A enésima fracção reduzida, obtida cortando a fracção contínua

$b_0+\displaystyle\frac{a_1}{b_1+\displaystyle\frac{a_2}{\begin{array}{cccc}b_{2}+ & & \\& \ddots & & \\& & +\displaystyle\frac{a_{n-1}}{b_{n-1}+\displaystyle\frac{a_{n}}{b_{n}}} & \\ & & & \ddots\end{array}}},$

pelos elementos $a_n,b_n$ , é uma expressão do tipo

$\displaystyle\frac{p_n}{q_n}=b_0+\displaystyle\frac{a_1}{b_1+\displaystyle\frac{a_2}{\begin{array}{ccc}b_{2}+ & & \\& \ddots & \\& & +\displaystyle\frac{a_{n-1}}{b_{n-1}+\displaystyle\frac{a_{n}}{b_{n}}}\end{array}}}=b_{0}+\displaystyle\mathcal{K}_{j=1}^{n }\left( \frac{a_{j}}{b_{j}}\right)$

$=b_{0}+\dfrac{a_{1}}{b_{1}+}\dfrac{a_{1}}{b_{1}+}\cdots \dfrac{a_{n}}{b_{n}}$ .

FORMULÁRIO

Equações cúbicas, Equações quárticas, Formulário do 9.º ano, Formulário do 12.º ano, Trigonometria, Derivadas, Primitivas imediatas, Matemática discreta, Teoria dos números e Métodos numéricos.

Equações cúbicas

$ax^{3}+bx^{2}+cx+d=0\qquad$ com $a\neq 0$

Equação cúbica reduzida:

$t^{3}+pt+q=0\qquad$

cujos coeficientes são:

$p=\dfrac{c}{a}-\dfrac{b^{2}}{3a^{2}}\qquad$

$q=\dfrac{2b^{3}}{27a^{3}}-\dfrac{bc}{3a^{2}}+\dfrac{d}{a}$

Discriminante:

$\Delta =q^{2}+\dfrac{4p^{3}}{27}$

Uma solução da equação reduzida é:

$t_{1}=\left( -\dfrac{q}{2}+\dfrac{1}{2}\sqrt{q^{2}+\dfrac{4p^{3}}{27}}\right) ^{1/3}+\left( -\dfrac{q}{2}-\dfrac{1}{2}\sqrt{q^{2}+\dfrac{4p^{3}}{27}}\right) ^{1/3}$

As três soluções da equação em $x$ são:

$x_{1}=\left( -\dfrac{q}{2}+\dfrac{1}{2}\sqrt{q^{2}+\dfrac{4p^{3}}{27}}\right) ^{1/3}+\left( -\dfrac{q}{2}-\dfrac{1}{2}\sqrt{q^{2}+\dfrac{4p^{3}}{27}}\right) ^{1/3}-\dfrac{b}{3a}$

$x_{2}=-\dfrac{t_{1}}{2}+\sqrt{\dfrac{t_{1}^{2}}{4}+\dfrac{q}{t_{1}}}-\dfrac{b}{3a}$

$x_{3}=-\dfrac{t_{1}}{2}-\sqrt{\dfrac{t_{1}^{2}}{4}+\dfrac{q}{t_{1}}}-\dfrac{b}{3a}$

No caso do discriminante ser negativo, $p<0$ , as soluções da equação são

$x_{1}=2\sqrt{-\dfrac{p}{3}}\cos \left( \dfrac{1}{3}\arccos \left( -\dfrac{q}{2}\sqrt{-\dfrac{27}{p^{3}}}\right) \right) -\dfrac{b}{3a}$

$x_{2}=2\sqrt{-\dfrac{p}{3}}\cos \left( \dfrac{1}{3}\arccos \left( -\dfrac{q}{2}\sqrt{-\dfrac{27}{p^{3}}}\right) +\dfrac{2\pi }{3}\right) -\dfrac{b}{3a}$

$x_{3}=2\sqrt{-\dfrac{p}{3}}\cos \left( \dfrac{1}{3}\arccos \left( -\dfrac{q}{2}\sqrt{-\dfrac{27}{p^{3}}}\right) +\dfrac{4\pi }{3}\right) -\dfrac{b}{3a}$

Equações quárticas

$ax^{4}+bx^{3}+cx^{2}+dx+e=0\qquad$ com $a\neq 0$

equação reduzida

$y^{4}+Ay^{2}+By+C=0\qquad$

sendo os seus coeficientes dados por

$A=\dfrac{c}{a}-\dfrac{3b^{2}}{8a^{2}}$

$B=\dfrac{d}{a}-\dfrac{bc}{2a^{2}}+\dfrac{b^{3}}{8a^{3}}$

$C=\dfrac{e}{a}-\dfrac{bd}{4a^{2}}+\dfrac{b^{2}c}{16a^{3}}-\dfrac{3b^{4}}{256a^{4}}$

As soluções da equação são:

$x_{1}=-\dfrac{1}{2}\sqrt{2s-A}+\dfrac{1}{2}\sqrt{-2s-A+\dfrac{2B}{\sqrt{2s-A}}}-\dfrac{b}{4a}$

$x_{2}=-\dfrac{1}{2}\sqrt{2s-A}-\dfrac{1}{2}\sqrt{-2s-A+\dfrac{2B}{\sqrt{2s-A}}}-\dfrac{b}{4a}$

$x_{3}=\dfrac{1}{2}\sqrt{2s-A}+\dfrac{1}{2}\sqrt{-2s-A-\dfrac{2B}{\sqrt{2s-A}}}-\dfrac{b}{4a}$

$x_{4}=\dfrac{1}{2}\sqrt{2s-A}-\dfrac{1}{2}\sqrt{-2s-A-\dfrac{2B}{\sqrt{2s-A}}}-\dfrac{b}{4a}$

em que $s$ é uma solução da equação cúbica auxiliar:

$8s^{3}-4As^{2}-8Cs+\left( 4AC-B^{2}\right) =0$

Do 9.º ano

Do 12.º ano

Trigonometria

$2\sin \left( n\alpha \right) \cos \alpha =\sin \left( \left( n+1\right) \alpha \right) +\sin \left( \left( n-1\right) \alpha \right)$

$\tan \dfrac{\theta }{2}=\dfrac{1-\cos \theta }{\sin \theta }$

$\arctan\left( \dfrac{u}{\sqrt{1-u^{2}}}\right) =\arcsin u$ .

$\arctan \left( x\right) =\arcsin \left( \sqrt{\dfrac{x^{2}}{1+x^{2}}}\right)$

$\arctan\left( \dfrac{\cos\theta }{1+\sin \theta }\right) =\dfrac{1}{2}\left( \dfrac{\pi }{2}-\theta\right)$

Fórmula de Herão: a área $S$ de um triângulo conhecido o seu semi-perímetro $p$ e o comprimento dos lados $a,b$ e $c$ :

$S=\displaystyle\sqrt{p(p-a)(p-b)(p-c)}$

Derivadas

De FERREIRA, Jaime Campos, Curso de Matemáticas Gerais, IST, Ed. Secção de Folhas da AEIST, 1968-69.

Mais derivadas

$\dfrac{d}{dt}\left[ u\left( t\right) \right] ^{v\left( t\right) }=v\left( t\right) \left[ u\left( t\right) \right] ^{v\left( t\right) -1}u^{\prime }(t)+\left( \ln u\left( t\right) \right) \left[ u\left( t\right) \right] ^{v\left( t\right) }v^{\prime }(t)$

$\left( \dfrac{dz}{dt}\right) _{t_{0}}=\left( \dfrac{\partial z}{\partial x}\right) _{\left( x_{0},y_{0}\right) }\left( \dfrac{dx}{dt}\right) _{t_{0}}+\left( \dfrac{\partial z}{\partial y}\right) _{\left( x_{0},y_{0}\right) }\left( \dfrac{dy}{dt}\right) _{t_{0}}$

$\left( x^{x}\right) ^{\prime }=\left( 1+\ln x\right) x^{x}$

$\dfrac{d}{dt}\left( \displaystyle\int_{u(t)}^{v(t)}f\left( x,t\right) dx\right) =$

$=\displaystyle\int_{u\left( t\right) }^{v\left( t\right) }\dfrac{\partial f\left( x,t\right) }{\partial t}dx+f\left( v\left( t\right) ,t\right) v^{\prime }\left( t\right) -f\left( u\left( t\right) ,t\right) u^{\prime}\left( t\right)$

$\dfrac{d}{dt}\left( \displaystyle\int_{a}^{b}f\left( x,t\right) dx\right) =\displaystyle\int_{a}^{b}\dfrac{\partial f\left( x,t\right) }{\partial t}dx$

Primitivas Imediatas

De AGUDO, Dias e SILVA, Cândido, Matemáticas Gerais, Cálculo Integral, IST, Ed. Secção de Folhas da AEIST, 1965.

Matemática discreta

$\bigskip$

$\displaystyle\sum_{i=m}^{n}a_{i}=\sum_{i=m}^{n}A_{i+1}-A_{i}=A_{n+1}-A_{m}$

$\displaystyle\sum_{i=m}^{n-1}a_{i}=\sum_{i=m}^{n-1}A_{i+1}-A_{i}=A_{n}-A_{m}$

$\displaystyle\sum_{i=m}^{n}a_{i}=\sum_{i=m}^{n}A_{i}-A_{i+1}=A_{m}-A_{n+1}$

$\displaystyle\sum_{i=m}^{n-1}a_{i}=\sum_{i=m}^{n-1}A_{i}-A_{i+1}=A_{m}-A_{n}$

$\displaystyle\dbinom{n}{k}=\dbinom{n-1}{k}+\dbinom{n-1}{k-1}$

$\displaystyle\sum_{i=k}^{n}\dbinom{n}{i}^{2}\dbinom{i}{k}=\dbinom{n}{k}\dbinom{2n-k}{n}$

$\displaystyle\sum_{i=1}^{n}\dbinom{i}{1}+2\dbinom{i}{2}=\sum_{i=1}^{n}i^{2}$

$\displaystyle\sum_{i=r}^{n}\dbinom{i}{r}=\dbinom{n+1}{r+1}$

$\displaystyle\sum_{i=0}^{n}i^{2}=\displaystyle\frac{\left( n+1\right) n\left( 2n+1\right) }{6}$

$\displaystyle\sum_{i=0}^{n}i=\displaystyle\frac{n\left( n+1\right) }{2}$

$\displaystyle\sum_{i=n_{0}}^{n}\displaystyle\sum_{j=m_{0}}^{m}a_{ij}=\displaystyle\sum_{j=m_{0}}^{m}\displaystyle\sum_{i=n_{0}}^{n}a_{ij}$

$\displaystyle\sum_{i=0}^{n}\sum_{j=0}^{m}a_{ij}=\displaystyle\sum_{j=0}^{m}\sum_{i=0}^{n}a_{ij}$

$\displaystyle\sum_{i=0}^{n}\sum_{j=i}^{n}a_{ij}=\displaystyle\sum_{j=0}^{n}\displaystyle\sum_{i=0}^{j}a_{ij}$

$\displaystyle\sum_{i=0}^{n}\displaystyle\sum_{j=0}^{i}a_{ij}=\displaystyle\sum_{j=0}^{n}\sum_{i=j}^{n}a_{ij}$

$\displaystyle\sum_{i=0}^{n}\dbinom{n}{i}^{2}\sum_{k=0}^{i}\dbinom{i}{k}\dbinom{n}{k}\dbinom{2n-k}{k}=\sum_{k=0}^{n}\dbinom{n}{k}^{2}\dbinom{n+k}{k}^{2}.$

Teoria dos Números

Expoente do número primo $p$ na decomposição em números primos de $n!$ :

$\displaystyle\sum_{i\geq 1}\displaystyle\left\lfloor\dfrac{n}{p^i}\right\rfloor$

Dilogaritmo e função zeta $\zeta(n)$

$Li_{2}\left( 1\right) =\displaystyle\sum_{k=1}^{\infty }\dfrac{1}{k^{2}}=\zeta \left( 2\right) =\dfrac{\pi ^{2}}{6}$

$Li_{2}\left( x\right) =\displaystyle\sum_{k=1}^{\infty }\dfrac{x^{k}}{k^{2}}$

$Li_{2}\left( -1\right) =\displaystyle\sum_{k=1}^{\infty }\dfrac{\left( -1\right) ^{k}}{k^{2}}=-\displaystyle\sum_{k=1}^{\infty }\dfrac{\left( -1\right) ^{k+1}}{k^{2}}=-\dfrac{1}{2}\zeta \left( 2\right) =-\dfrac{\pi ^{2}}{12}$

$\displaystyle\sum_{k=1}^{\infty }\dfrac{\left( -1\right) ^{k+1}}{k^{n}}=\zeta \left( n\right) \left( 1-2^{1-n}\right)$

$\displaystyle\sum_{k=1}^{\infty }\dfrac{\left( -1\right) ^{k+1}}{k^{2}}=\dfrac{1}{2}\zeta\left( 2\right)$

Valoração $p$ -ádica de $\left( \dbinom{n}{k}\right)$

$v_{p}\left( \dbinom{n}{k}\right) =\displaystyle\sum_{i=1}^{\left\lfloor \log_{p}(n)\right\rfloor }\underset{0\text{ ou }1}{\underbrace{\left( \left\lfloor \dfrac{n}{p^{i}}\right\rfloor -\left\lfloor \dfrac{k}{p^{i}}\right\rfloor -\left\lfloor \dfrac{n-k}{p^{i}}\right\rfloor \right) }}\leq\left\lfloor \log _{p}(n)\right\rfloor$

Constante de Apéry

$\displaystyle\sum_{n=1}^{\infty }\dfrac{1}{n^{3}}=\dfrac{5}{2}\displaystyle\sum_{k=1}^{N}\dfrac{\left( -1\right) ^{k-1}}{k^{3}\dbinom{2k}{k}}.$

Série de Euler do Problema de Basileia

$\displaystyle\sum_{n=1}^{\infty }\dfrac{1}{n^{2}}=\displaystyle\int_{0}^{1}\left( \int_{0}^{1}\dfrac{d\tau }{1-t\tau }\right) \;dt=\dfrac{\pi ^{2}}{6}$ .

Métodos Numéricos

Método da secante de determinação da raiz de uma equação não linear

Em geral, para o inteiro $i=2,3,4\ldots$ obtemos, por este método, a aproximação

$x_{i+1}=x_{i}-f\left( x_{i}\right) \times\dfrac{x_{i}-x_{i-1}}{f\left( x_{i}\right) -f\left( x_{i-1}\right) }$

Método de Newton de determinação da raiz de uma equação não linear

Em geral, para o inteiro $i=1,2,3,\ldots$ obtemos, por este método, a aproximação

$x_{i+1}=x_{i}-\dfrac{f\left( x_{i}\right) }{f^{\prime }\left( x_{i}\right) }$

5 respostas a Formulário

Binca diz:

26 de Novembro de 2010 às 00:55

Gostaria de saber como integrar por partes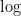 $\log {}$ neperiano com funcoes dentro , exemplo integral de $\ln (2x+1)dx$
Se usa substituicao ou partes? ou os dois?
Obrigada

Responder
- Américo Tavares diz:
  
  26 de Novembro de 2010 às 10:46
  
  O integral do logaritmo obtém-se pelo método de integração por partes
  
  $\displaystyle\int u^{\prime }(x)v(x)dx=u(x)v(x)-\int u(x)v^{\prime }(x)dx$
  
  $\displaystyle\int \ln xdx=\displaystyle\int 1\times \ln xdx=x\ln x-\displaystyle\int x\dfrac{1}{x}dx$
  
  $=x\ln x-x=(\ln x-1)x$
  
  No seu exemplo
  
  $\displaystyle\int \ln \left( 2x+1\right) dx$
  
  se fizer a substituição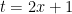 $t=2x+1$ , visto que 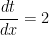$\dfrac{dt}{dx}=2$ , logo $\dfrac{dx}{dt}=\dfrac{1}{2}$ , vem
  
  $\displaystyle\int \ln \left( 2x+1\right) dx=\int \ln \left( t\right) \dfrac{1}{2}dt=\dfrac{1}{2}\displaystyle\int \ln tdt$
  $=\dfrac{1}{2}(\ln t-1)t=\dfrac{1}{2}(\ln \left( 2x+1\right) -1)\left( 2x+1\right)$
Junior diz:

19 de Agosto de 2011 às 17:40

Olá boa tarde. Sei que é chato mas, vim aqui no seu blog pedir parceria, pois acredito que com parceria os dois sites podem se beneficiar.
Estou propondo uma troca de link.. para o meu site http://oscursosonline.com -> Cursos online Grátis EAD
Caso você aceite pode colocar o link no seu site e nos avisar… que faremos o mesmo o mais rápido possível… no e-mail:parceria@oscursosonline.com
Caso não aceite, pedimos desculpas pelo incômodo.

Responder
Pedro diz:

22 de Junho de 2013 às 13:00

Caro Américo Tavares, na equação de 3º Grau vejo um erro, onde em vez de -q/2 aparece q/2

Deveria ser: $\sqrt[3]{\frac{-q}{2}+\frac{\sqrt{q^2+\frac{4p^3}{27}}}{2}} + \sqrt[3]{\frac{-q}{2}-\frac{\sqrt{q^2+\frac{4p^3}{27}}}{2}} - \frac{b}{3a}$

Em vez de $\sqrt[3]{\frac{q}{2}+\frac{\sqrt{q^2+\frac{4p^3}{27}}}{2}} + \sqrt[3]{\frac{q}{2}-\frac{\sqrt{q^2+\frac{4p^3}{27}}}{2}} - \frac{b}{3a}$

Responder
- Américo Tavares diz:
  
  22 de Junho de 2013 às 18:03
  
  Obrigado, corrigido.

Deixe um comentário Cancelar resposta

Este site utiliza o Akismet para reduzir spam. Fica a saber como são processados os dados dos comentários.

	Louis Augusto em Conjectura de Collatz ou probl…
	Arthur Antônio. em Perímetro da astróide
	Arthur Antônio. em Perímetro da astróide
	Tarso Coelho em A Matemática é uma Ciência? ::…
	António Ferrão em Redes Neuronais Artificiais
	maria eclair em Exercício de aplicação dos teo…
	Carlos Alberto Guima… em Resolução da equação do 3.º gr…
	Carlos Alberto Guima… em Resolução da equação do 3.º gr…
	Carlos Alberto Guima… em Resolução da equação do 3.º gr…
	Carlos Alberto Guima… em Resolução da equação do 3.º gr…

	Louis Augusto em Conjectura de Collatz ou probl…
	Arthur Antônio. em Perímetro da astróide
	Arthur Antônio. em Perímetro da astróide
	Tarso Coelho em A Matemática é uma Ciência? ::…
	António Ferrão em Redes Neuronais Artificiais
	maria eclair em Exercício de aplicação dos teo…
	Carlos Alberto Guima… em Resolução da equação do 3.º gr…
	Carlos Alberto Guima… em Resolução da equação do 3.º gr…
	Carlos Alberto Guima… em Resolução da equação do 3.º gr…
	Carlos Alberto Guima… em Resolução da equação do 3.º gr…

Formulário

FORMULÁRIO

Do 9.º ano

Do 12.º ano

Trigonometria

Derivadas

Primitivas Imediatas

Matemática discreta

Teoria dos Números

Métodos Numéricos

Partilhar isto:

5 respostas a Formulário

Deixe um comentário Cancelar resposta

Pesquisar

math.SE

Follow Blog via Email

Últimos Comentários e respostas

Some contributions to math.SE

Blogue filiado em

Colaboração de

Estatísticas do site

Países de origem

Categorias (Temas)

Entradas mais populares

Hiperligações

Física

Fractais

LaTeX e MathJax

Matemática

Matemática/Computação

Matemática/Perguntas e Respostas

Matemática/Problemas e Exercícios

Matemática/Referências

Meu outro Blogue

z.Diversos

Etiquetas

Arquivos

Follow Blog via Email

Arquivos

Colaboração de

Comentários Recentes

Artigos & páginas mais populares

Comentários

LaTeX

Metadados