(Daqui e daqui)
Enunciado do Problema
Seja  o maior inteiro positivo tal que
o maior inteiro positivo tal que 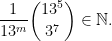 Determine, justificando, um majorante de
Determine, justificando, um majorante de 
- Afirmação não demonstrada: 10 é um majorante de
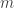 . Encontre um mais pequeno.
. Encontre um mais pequeno.
Problem Statement
Let  be the greatest positive integer such that
be the greatest positive integer such that 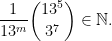 Find with proof an upper bound for
Find with proof an upper bound for 
- Claim: 10 is an upper bound for
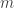 . Find a smaller one.
. Find a smaller one.

Solution par Pierre Bernard, France
On sait que

De plus, chaque terme
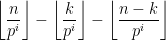
vaut 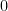 ou
ou 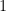 (on a toujours
(on a toujours  qui vaut
qui vaut 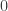 ou
ou 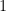 ).
).
Si 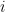 est assez grand, il est clair que
est assez grand, il est clair que
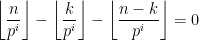 .
.
Précisément, puisque 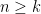 , il suffit que
, il suffit que  , c’est-à-dire
, c’est-à-dire  pour que
pour que
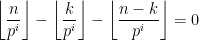 .
.
On a donc:

Donc

Et  c’est mieux que
c’est mieux que 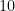 :)
:)

* * *

Solution by Pierre Bernard, France; translated by Américo Tavares
We know that

Furthermore, each term
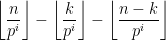
is 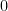 or
or 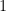 (we have allways
(we have allways  which is
which is 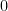 or
or 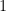 ).
).
For 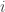 sufficiently large it is clear that we have
sufficiently large it is clear that we have
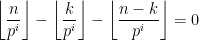 .
.
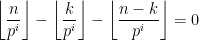 .
.
Therefore
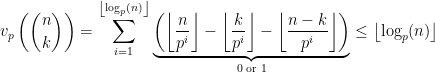
Thus

And  is better than
is better than 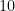 :)
:)
Other solvers: fede (comments in Gaussianos‘s blog) and fatima

* * *

Resolução de Pierre Bernard, França; tradução de Américo Tavares.
Sabe-se que

Além disso, cada termo
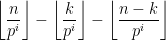
vale 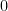 ou
ou 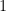 (tem-se sempre
(tem-se sempre  que é igual a
que é igual a 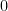 ou
ou 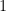 ).
).
Para 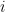 suficientemente grande é claro que se tem
suficientemente grande é claro que se tem
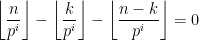 .
.
Ora, dado que 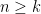 , é suficiente que
, é suficiente que  , isto é
, isto é  para se ter
para se ter
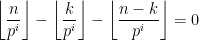 .
.
Portanto:

Deste modo

E  é melhor do que
é melhor do que 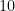 :)
:)
Outros: fede (commentários no blogue Gaussianos) e fatima

* * *

Notas:
1. 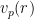 designa a valoração (ou valorização)
designa a valoração (ou valorização)  -ádica (valuation
-ádica (valuation  -adique) de
-adique) de  : o expoente do número primo
: o expoente do número primo  na decomposição em factores primos do inteiro
na decomposição em factores primos do inteiro  . Por outras palavras,
. Por outras palavras,  divide
divide  mas
mas 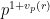 não divide
não divide  .
.
2. Também se usa a notação 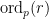 (ordem ou ordinal de
(ordem ou ordinal de  em
em  ) com o mesmo significado.
) com o mesmo significado.
3. 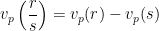 (com
(com  ).
).
4. Teorema de Legendre: Qualquer que seja o inteiro positivo 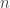 , o expoente do número primo
, o expoente do número primo  na decomposição em números primos de
na decomposição em números primos de 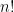 é igual a
é igual a


Remarks:
1. 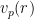 denotes the
denotes the  -adic valuation of
-adic valuation of  : the exponent of the prime
: the exponent of the prime  in the factorization into prime numbers of the integer
in the factorization into prime numbers of the integer  . In other words
. In other words  divides
divides  and
and 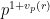 does not divide
does not divide  .
.
2. With the same meaning another notation is also used: 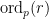 (order or ordinal of
(order or ordinal of  at
at  )
)
3. 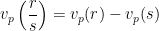 (with
(with  ).
).
4. Theorem (Legendre): For every positive integer  , the exponent of the prime number
, the exponent of the prime number  in the factorization into prime numbers of
in the factorization into prime numbers of 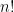 is
is

.
e
e reduza-o ao cálculo do volume, entre
e
, do parabolóide de secção circular





 (De:
(De: 











