Desigualdade probabilística de Hoeffding ilustrada com um caso específico simples

No artigo (de Machine Learning) de Sébastien Bubeck e Mark Sellke A Universal Law of Robustnesss via Isoperimetry é utilizada a desigualdade de Hoeffding, [Hoeffding, Wassily (1963)] na demonstração do teorema principal. Esta desigualdade probabilística apresenta o seguinte enunciado, em tradução do original

Desigualdade de Hoeffding [Hoeffding, Wassily (1963) Theorem 2]: Se $X_{1},X_{2}\dots,X_{n}$ forem variáveis aleatórias independentes e $a_{i}\leq X_{i}\leq b_{i}$ , $i=1,2\ldots,n$ , então, para $t>0$ :

$\mathbb{P}\left[\overline{X}-\mu\geq t\right]\leq\exp\left(-2n^2t^2/\sum_{i=1}^{n}\left(b_{i}-a_{i}\right)\right)^2.$

Notação: $\overline{X}=\dfrac{S}{n}$ e $\mu =\mathbb{E}\left[ \overline{X}\right] =\dfrac{\mathbb{E}\left[ S\right]}{n}$ , em que a soma $S=\sum_{i=1}^{n}X_{i}$ e $\mathbb{E}\left[\overline{X}\right]$ é a esperança matemática de $\overline{X}$ .

Embora a demonstração deste teorema não faça referência explícita à desigualdade de Markov, no caso particular do exercício que apresento a seguir, vou usá-la para facilitar a sua demonstração, à semelhança do que é feito neste vídeo de MIT RES.6-012 Introduction to Probability. No exercício, à excepção da utilização da desigualdade de Markov, sigo, para mais fácil generalização, os passos da demonstração do teorema original adaptada ao caso apresentado.

Desigualdade de Markov: se $Z$ for uma variável aleatória positiva ou nula cuja esperança matemática se designa por $\mathbb{E}[Z]$ e $c$ uma constante positiva, então

$\mathbb{P}\left( Z\geq c\right) <\dfrac{\mathbb{E}\left[ Z\right] }{c}.$

Exercício (caso particular da desigualdade de Hoeffding): Sejam $X_{1}$ , $X_{2}$ , $\dots$ , $X_{n}$ variáveis aleatórias independentes que tomam, com igual probabilidade, os valores $-1$ e $1$

$\mathbb{P}\left( X_{i}=-1\right) =\mathbb{P}\left(X_{i}=1\right)=1/2,\qquad i=1,\ldots ,n.$

Designando a média das variáveis aleatórias por $\overline{X}=S/n$ , em que $S=\sum_{i=1}^{n}X_{i}$ é a sua soma, e fazendo uso da desigualdade de Markov, determine o seguinte majorante da probabilidade da média ser pelo menos $t$

$\mathbb{P}\left[ \overline{X}\geq t\right] \leq e^{-nt^{2}/2},\qquad t>0.\qquad\qquad(1)$

Resolução: Se substituirmos $\overline{X}$ em $\mathbb{P}\left[ \overline{X}\geq t\right]$ , obtemos a probabilidade equivalente

$\mathbb{P}\left[\overline{X}\geq t\right]=\mathbb{P}\left[\dfrac{S}{n}\geq t\right]=\mathbb{P}\left[S\geq nt\right].$

Seja, agora, $h$ uma constante positiva arbitrária. Como a condição $S\geq nt$ é equivalente a $e^{hS}\geq e^{hnt}$ , podemos escrever

$\mathbb{P}\left[ \overline{X}\geq t\right]=\mathbb{P}\left[ S\geq nt\right]=\mathbb{P}\left[ e^{hS}\geq e^{hnt}\right].$

Para majorar esta última probabilidade usamos a desigualdade de Markov,
que aplicada a este caso se traduz em

$\mathbb{P}\left[ e^{hS}\geq e^{hnt}\right] \leq \dfrac{\mathbb{E}\left[ e^{hS}\right]}{e^{hnt}}.\qquad\qquad\qquad(2)$

Substituindo o valor de $S$ , tem-se

$\dfrac{\mathbb{E}\left[e^{hS}\right]}{e^{hnt}}=\dfrac{\mathbb{E}\left[e^{h\left(\sum_{i=1}^{n}X_{i}\right)}\right]}{e^{hnt}}=\dfrac{\displaystyle\prod\limits_{i=1}^{n}\mathbb{E}\left[e^{hX_{i}}\right]}{e^{hnt}}.\qquad(3)$

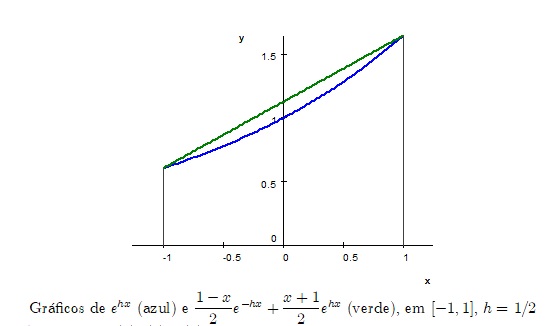
Dado que a função exponencial $f(x)=e^{hx}$ é convexa, o seu gráfico é limitado superiormente, no intervalo $\left[ -1,1\right]$ , pela recta que une os pontos $\left( -1,f(-1)\right) =\left(-1,e^{-h}\right)$ e $\left( 1,f(1)\right) =\left( 1,e^{h}\right)$ , cuja equação é dada por

$y=\dfrac{1-x}{2}e^{-h}+\dfrac{x+1}{2}e^{h}.$

Assim,

$f(x)=e^{hx}\leq\dfrac{1-x}{2}e^{-h}+\dfrac{x+1}{2}e^{h},\qquad x\in \left[-1,1\right],\qquad(4)$

pelo que $\mathbb{E}\left[ e^{hX_{i}}\right] =\mathbb{E}\left[ f(X_{i})\right]$ satisfaz a condição

$\mathbb{E}\left[e^{hX_{i}}\right]\leq\dfrac{1-\mathbb{E}\left[X_{i}\right]}{2}e^{-h}+\dfrac{\mathbb{E}\left[X_{i}\right]+1}{2}e^{h}=\dfrac{1}{2}\left(e^{-h}+e^{h}\right),\qquad(5)$

atendendo a que $\mathbb{E}\left[ X_{i}\right] =0$ , pois a distribuição de cada $X_{i}$ é simétrica.

De $(2),(3)$ e $(5)$ resulta então

$\mathbb{P}\left[\overline{X}\geq t\right]\leq\dfrac{\prod\limits_{i=1}^{n}\mathbb{E}\left[ e^{hX_{i}}\right] }{e^{hnt}}\leq\left(\dfrac{e^{-h}+e^{h}}{2e^{ht}}\right)^{n}.\qquad(6)$

Para facilitar o resto do cálculo, vamos agora reescrever $\left(^{-h}+e^{h}\right)/2$ :

$\dfrac{e^{-h}+e^{h}}{2}=e^{-h-\ln 2+\ln\left(1+e^{2h}\right)}:= e^{L\left(h\right)},\qquad\qquad(7)$

em que o expoente $L\left( h\right) =-h-\ln 2+\ln\left(1+e^{2h}\right)$ . As duas primeiras derivadas de $L\left( h\right)$ são

$L^{\prime }\left( h\right)=-1+\dfrac{2}{1+e^{-2h}}\qquad\text{e\qquad }L^{\prime\prime}\left(h\right)=\dfrac{4e^{-2h}}{\left(1+e^{-2h}\right)^{2}}.$

A segunda derivada admite a seguinte factorização

$L^{\prime \prime }\left( h\right) =4\times\dfrac{1}{e^{-2h}+1}\times\dfrac{e^{-2h}}{e^{-2h}+1}=4\times\dfrac{1}{e^{-2h}+1}\left(1-\dfrac{1}{e^{-2h}+1}\right),\qquad(8)$

isto é, $L^{\prime \prime }\left( h\right) =4u(1-u)$ em que $u=1/(e^{-2h}+1)\in \left] 0,1\right[$ , uma vez que $0<1/(e^{-2h}+1)<1$ . Ora, o máximo de $4u(1-u)$ ocorre quando $u=1/2$ , donde $L^{\prime\prime}\left( h\right) \leq 4\times (1/2)(1-1/2)=1$ . Pelo desenvolvimento em série de Taylor, dado que $L\left( 0\right) =L^{\prime }\left(0\right) =0$ , vem

$L\left(h\right)=L(0)+L^{\prime}\left(0\right)h+\dfrac{L^{^{\prime \prime}}\left(0\right) }{2}h^{2}+\cdots \leq \dfrac{1}{2}h^{2}.\qquad(9)$

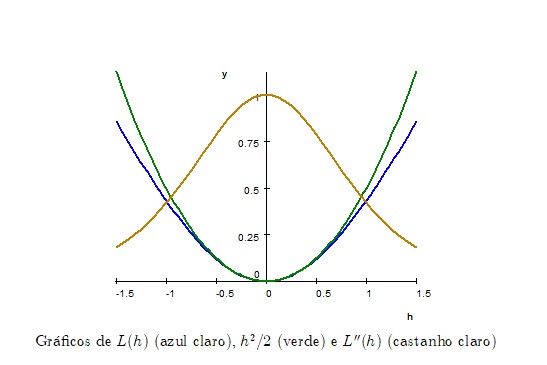
No gráfico anterior mostram-se os andamentos de $L(h)$ , $h^{2}/2$ e $L^{\prime \prime }(h)$ . De $(7)$ e $(9)$ , resulta que $\left( e^{-h}+e^{h}\right) /2=e^{L\left( h\right) }\leq e^{h^{2}/2}$ , e de $(6)$ ,

$\mathbb{P}\left[\overline{X}\geq t\right] \leq \left(\dfrac{e^{-h}+e^{h}}{2e^{ht}}\right) ^{n}\leq e^{-hnt+nh^{2}/2}.\qquad(10)$

Designe-se o expoente de $(10)$ por $g(h)=-hnt+nh^{2}/2$ . Visto que $\min_{h}\exp\left[g(h)\right]=\exp\left[\min_{h}g(h)\right]$ e $g^{\prime }(h)=nh-nt=0$ , o segundo membro de $(10)$ tem o mínimo em $h_{\min }=t$ . Finalmente, inserindo este valor em $(10)$ , obtemos o majorante $e^{-hnt+nh^{2}/2}=e^{-nt^{2}/2}$ de $\mathbb{P}\left[ \overline{X}\geq t\right]$ indicado em $(1)$ , o que demonstra a desigualdade de Hoeffding, neste caso específico.

Apresentam-se dois exemplos gráficos para os casos $t=1/2$ e $t=3/4$ .

[Hoeffding, Wassily (1963)] Probability inequalities for sums of bounded random variables (PDF). Journal of the American Statistical Association. 58 (301): 13–30. Acessível via Wikipedia

hoeffding-exercicio Descarregar

Sobre Américo Tavares

eng. electrotécnico reformado / retired electrical engineer

Ver todos os artigos de Américo Tavares →

	Louis Augusto em Conjectura de Collatz ou probl…
	Arthur Antônio. em Perímetro da astróide
	Arthur Antônio. em Perímetro da astróide
	Tarso Coelho em A Matemática é uma Ciência? ::…
	António Ferrão em Redes Neuronais Artificiais
	maria eclair em Exercício de aplicação dos teo…
	Carlos Alberto Guima… em Resolução da equação do 3.º gr…
	Carlos Alberto Guima… em Resolução da equação do 3.º gr…
	Carlos Alberto Guima… em Resolução da equação do 3.º gr…
	Carlos Alberto Guima… em Resolução da equação do 3.º gr…

	Louis Augusto em Conjectura de Collatz ou probl…
	Arthur Antônio. em Perímetro da astróide
	Arthur Antônio. em Perímetro da astróide
	Tarso Coelho em A Matemática é uma Ciência? ::…
	António Ferrão em Redes Neuronais Artificiais
	maria eclair em Exercício de aplicação dos teo…
	Carlos Alberto Guima… em Resolução da equação do 3.º gr…
	Carlos Alberto Guima… em Resolução da equação do 3.º gr…
	Carlos Alberto Guima… em Resolução da equação do 3.º gr…
	Carlos Alberto Guima… em Resolução da equação do 3.º gr…